Page 35 - progetto alice

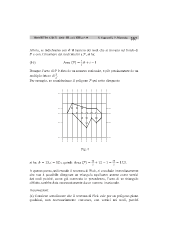
PROGETTO ALICE 2012 - III • •• • vol. XIII • •• • n° 39 S. Capparelli, P. Maroscia Allora, se indichiamo con X il numero dei nodi che si trovano sul bordo di W e con i il numero dei nodi interni a W, si ha: (16) YZV[W X! \ Dunque l’area di W è data da un numero razionale, e più precisamente da un multiplo intero di . Per esempio, se consideriamo il poligono W qui sotto disegnato: Fig. 4 ] si ha: X (? \ H e quindi: YZV[W !H R?). A questo punto, utilizzando il teorema di Pick, si conclude immediatamente che non è possibile disegnare un triangolo equilatero avente come vertici dei nodi poiché, come già osservato in precedenza, l’area di un triangolo siffatto sarebbe data necessariamente da un numero irrazionale. Osservazioni: (a) Conviene sottolineare che il teorema di Pick vale per un poligono piano qualsiasi, non necessariamente convesso, con vertici nei nodi, purché